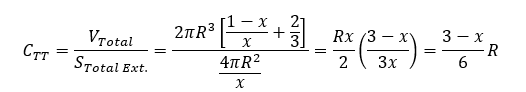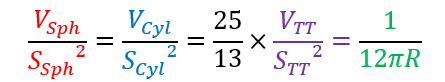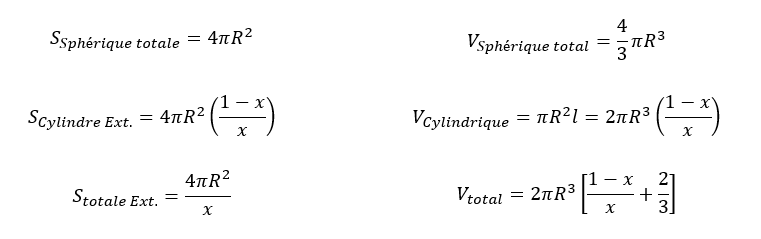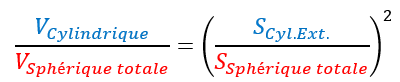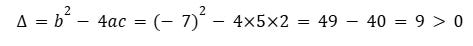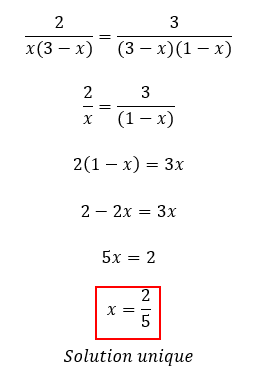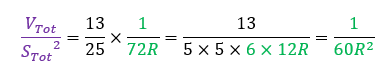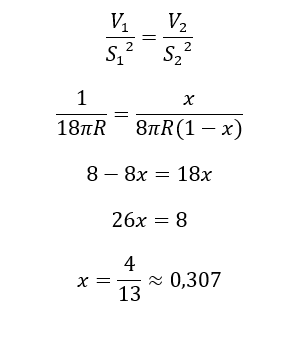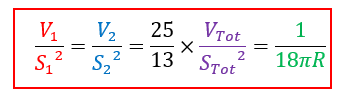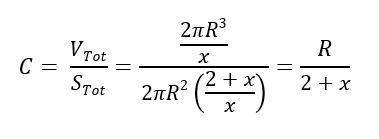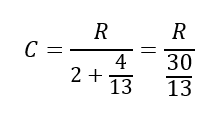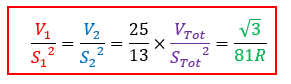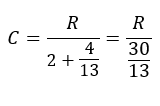Exclusif / G. Pierrez, Ingénieur : La Géométrie Cachée de l'Ovni du Nimitz
Guillaume Pierrez a trouvé un étrange ratio semblant guider la forme de cet ovni cylindrique observé en 2004 par la marine américaine
Une forme au mépris de l’aérodynamisme
Lors d’une course de Formule 1 seriez-vous prêt à miser sur un participant se présentant avec de roues carrées ? Probablement que non…
Pourtant c’est à peu prêt le genre de pari que les concepteurs du TIC TAC (si conception il y a) auraient pu tenir.
Dans le cadre d’un projet de conception d’un avion supersonique, n’importe quel ingénieur en aéronautique partirait sur une forme en pointe de flèche. C’est en effet ce que la mécanique des fluides préconise afin de favoriser l’écoulement de l’air et de minimiser l’échauffement du fuselage. Il est donc parfaitement invraisemblable de retenir la forme d’un TIC TAC pour un mobile présentant cette capacité.
Bien que l’on ignore sa technique de vol, nous savons donc déjà une chose essentielle : la forme semble prévaloir sur l’aérodynamisme.
Le phénomène est-il issu d’une conception ?
Avant de poursuivre, il convient de confirmer ou d’infirmer l’artificialité du phénomène. Certains invoqueront à juste titre que le comportement décrit par les témoins, les cinétiques, et bien d’autres aspects ne laissent aucun doute sur le caractère artificiel du phénomène. Il est vrai que l’ensemble de ces éléments constituent un très fort faisceau de présomption.
Toutefois, je pense qu’une approche plus technique et objective est envisageable. Laissez-moi vous l’expliquer à l’aide d’une canette de soda.
Songez à votre canette de soda en aluminium. Pensez un instant à ceux qui l’ont conçu et à la toute première question qu’ils ont dû se poser :
« Quelles sont les dimensions qui offrent un volume optimal pour un coût en aluminium minimal ? »
Si l’on considère qu’une canette est grossièrement assimilable à un cylindre, on peut décrire son volume et sa surface à partie de son rayon R et de sa hauteur h. Puis établir une relation entre Volume, coût et surface. Sans entrer dans les détails, les mathématiques permettent de trouver la solution idéale.
Ce faisant, la canette obtenue porte littéralement la « trace mathématique » de son artificialité dans ses dimensions :
Imaginez à présent un archéologue du futur qui retrouvera le vestige de votre canette. Il pourra en mesurer les dimensions et effectuera le raisonnement inverse pour enfin constater avec certitude l’effort d’optimisation. Car il existe un très grand nombre de possibilité mais une seule est optimisée ! En toute logique, il en conclura que cet objet fut conçu et produit par des personnes astucieuses.
Ainsi, si l’on considère que l’objet est artificiel et conçu de façon astucieuse, il est peut-être possible de retrouver une « trace d’optimisation » dans sa géométrie et ses dimensions tout comme notre archéologue a su retrouver une trace d’optimisation dans la forme de notre canette … A contrario, si l’on ne trouve rien de probant, le mystère restera entier …
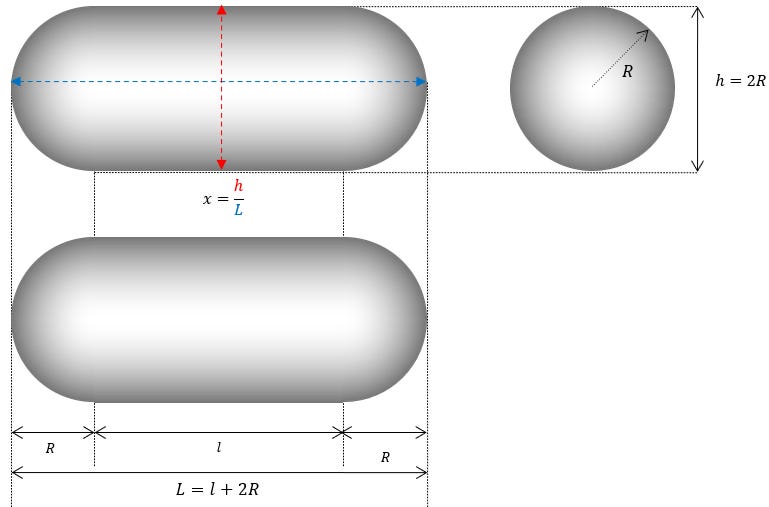
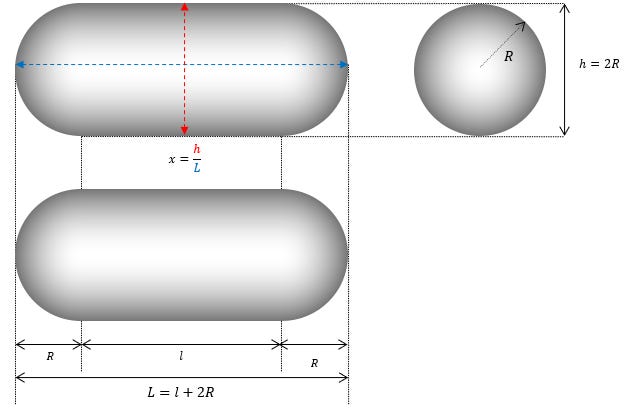
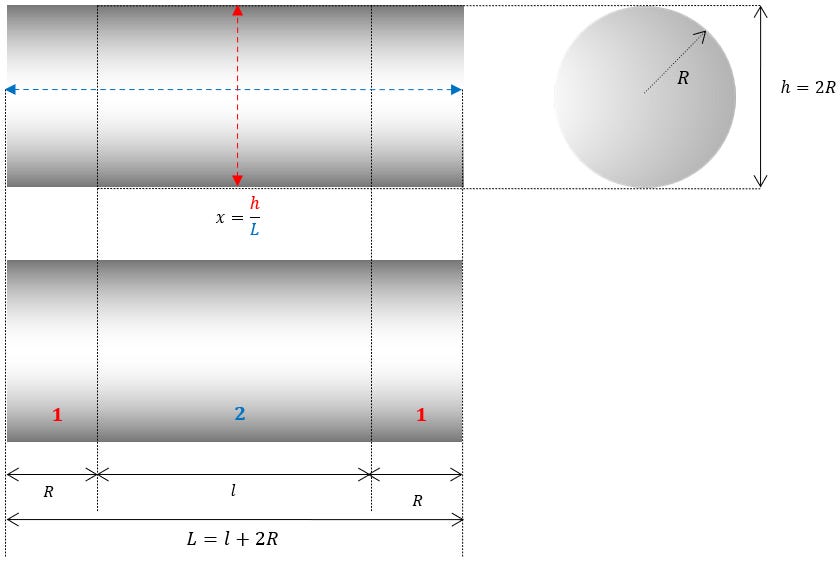
Pour commencer, notons que la forme d’un TIC TAC ne nécessite que deux paramètres ( R et x ) pour définir toutes les solutions possibles :
Calcul de l en annexe 1.
A ce stade on peut constater que la géométrie du phénomène comporte deux types de surfaces distinctes :
Ce constat peut paraître trivial mais il est s’avérera essentiel par la suite.
- Une surface cylindrique (côté du cylindre apparaissant en bleu)
- Deux surfaces sphériques (demies sphères aux extrémités en rouge)
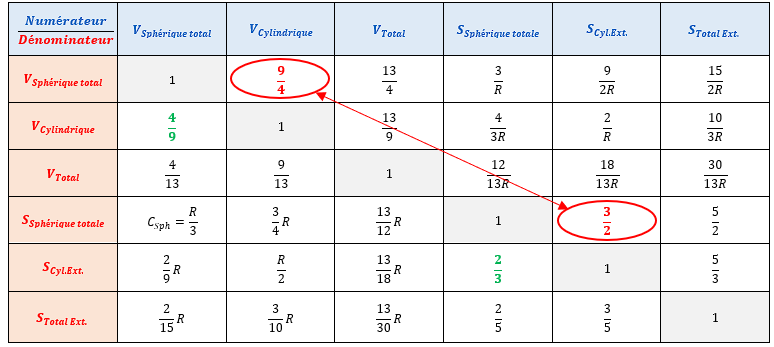
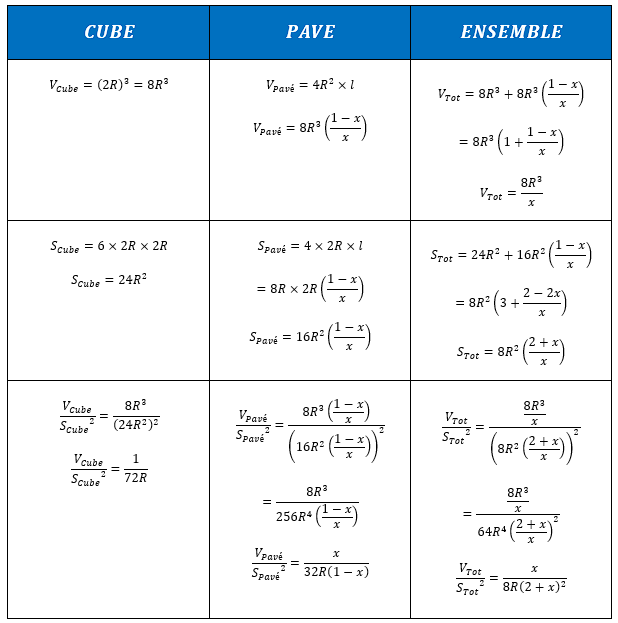
A présent, décrivons mathématiquement les volumes et les surfaces de chacune de ces parties et comparons-les entre elles à l’aide d’une matrice (détails des calculs disponibles en annexe 2) :
Rien de particulier ne ressort véritablement de cet essai. De fait lorsque R et x sont indéterminés, aucune relation probante ne semble clairement émerger.
Essayons à présent la même démarche en introduisant une des deux valeurs x ou R. Il n’est pas possible de donner une estimation de R suffisamment précise en revanche en se basant sur les images visibles de la vidéo FLIR 1 il est possible de donner un encadrement de x :
Les images en spectre visible sont plus précises que celles en spectre IR qui ont tendance à « baver ».
Reprenons donc notre tableau précédent avec x= 0,4 :
Pour la valeur de x=0,4 , la matrice de comparaison fait à présent émerger une relation singulière liant les volumes et les surfaces des parties :
Qui peut également s’écrire sous la forme plus élégante :
Par commodité, cette relation sera désignée V/S² par pour la suite de l’étude.
A ce stade, il peut seulement être affirmé que la forme observée présente effectivement une relation géométrique singulière qui n’apparaît que pour le rapport hauteur sur longueur observé c’est-à-dire pour x= 0,4 (vérification disponible en Annexe 3) :
La résolution de la relation V/S² mène à une solution particulière de x correspondant précisément à la valeur observée sur la vidéo. Il est donc très improbable que cette solution particulière apparaisse de façon fortuite.
Ce constat tend à démontrer que l’objet est bien le fruit d’une conception astucieuse dont la nature pourrait être en lien avec la relation V/S² . Si c’est bien le cas, cette relation serait donc également le point de départ de la conception du fuselage.
Nous verrons par la suite que la relation est en réalité la conséquence d’une relation plus générale ce qui exclue de facto la possibilité d’une coïncidence. Néanmoins en parler ici rendrait le raisonnement anachronique.
Peut-il s’agir d’une coïncidence fortuite ?
Si faible soit-elle, la possibilité d’une coïncidence doit être envisagée mais l’étau se resserre à nouveau lorsque l’on étudie l’aspect de la compacité :
La compacité se définie par le rapport entre le volume d’un objet et sa surface. Elle permet de comparer la capacité des formes géométriques à englober un volume maximal à l’intérieur d’une surface minimale.
Pour illustration, la sphère est la forme la plus performante avec une compacité de :
Déterminons la compacité de la forme TIC TAC :
Ce qui, pour :
devient :
Il nous manque à présent une estimation de pour donner une valeur approchée de CTT.
Rappelons que les pilotes ont estimé la longueur du Tic-Tac à environ 40 ft soit environ 12m.
Rappelons également la définition de L sur le schéma : L= l+2R
Soit :
Ce qui pour :
donne :
On peut alors donner une estimation de la compacité du Tic-Tac :
Ce résultat ne nous donne aucune certitude et ne permet ici que des spéculations difficilement vérifiables mais qui méritent néanmoins d’être présentées.
L’estimation des 40 ft de long du pilote contient bien évidemment une incertitude à laquelle s’ajoute celle de la conversion de ft à m. On peut donc raisonnablement se demander si la compacité réelle ne serait pas de 1.
Si on considère que :
Alors :
La longueur serait alors de :
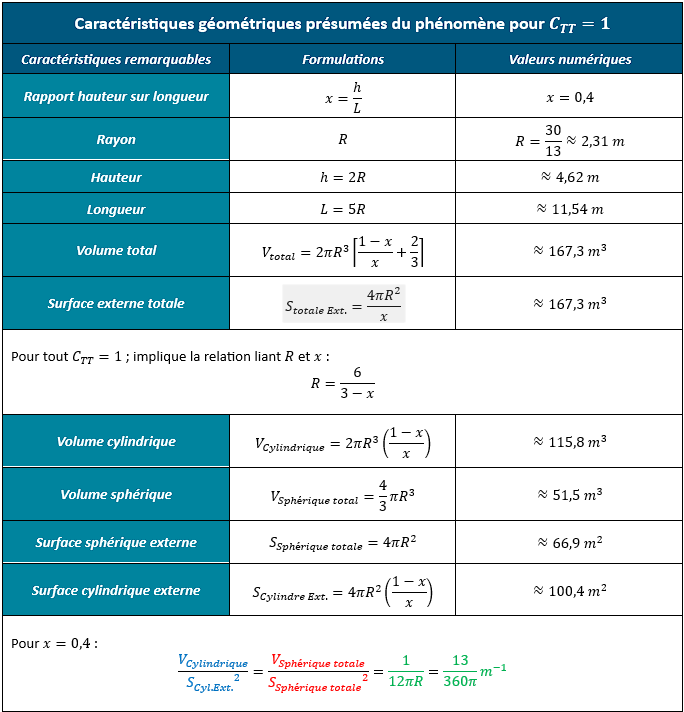
Ce qui correspondrait approximativement à 38 ft et s’avère compatible avec l’observation faite par les pilotes. Sur la base de cette hypothèse, on peut donc compléter le schéma initial et se risquer à donner une prédiction approchée des dimensions du phénomène :
Il est bien sûr étonnant de constater que deux raisonnements distincts puissent mener à des prédictions concordantes tant vis-à-vis de la vidéo (valeur de x=0,4) que de l’estimation de la longueur des pilotes (11,54 m contre 12,19 m). Cette concordance est en soit réellement confondante et tend à priori en faveur d’une conception judicieuse.
A toutes fins utiles les valeurs numériques des autres aspects géométriques sont résumées ci-après :
Voici qui conclue la première partie.
La seconde partie s’avère plus difficile à expliquer et bien plus mathématiques mais c’est également celle qui a mon sens est à la fois la plus convaincante et la plus stupéfiante.
Que peut-on apprendre de la relation V/S² ?
Rappelons la relation :
Sous cette forme nous ne pouvons pas apprendre grand-chose de plus. Il nous faut introduire un nouvel aspect comme l’expression du volume et de la surface de l’ensemble. L’idée est simple et le résultat se démontre très facilement (démonstration disponible en annexe 4) :
On obtient donc cette triple relation qui nous apprend que d’un point de vue géométrique l’ensemble de la forme est également en relation avec les différentes parties. Visiblement, les contraintes sont encore plus spécifiques qu’on ne l’imaginait jusqu’ici.
Elle fait également apparaitre le coefficient 25/13 … qui, à ma connaissance, ne correspond à aucune constante de la physique. Malgré mes recherches dans la littérature et les aides mémoires d’ingénierie, je ne trouve aucune correspondance tant pour la relation que pour le coefficient 25/13.
La relation laisse toutefois « envisager » un flux (possiblement de nature électromagnétique) s’échangeant entre les différents volumes au travers des différentes parois mais il s’agit là d’une interprétation personnelle purement spéculative. La motivation de cette relation pourrait tout aussi bien être d’ordre esthétique après tout.
Si, comme pour moi, la démarche vous paraît intéressante jusqu’à présent, c’est ici qu’elle devient véritablement déroutante ! je vous laisse en juger par vous-même :
Je vous passe les détails personnels m’ayant mené à cette idée afin de vous mener directement aux résultats :
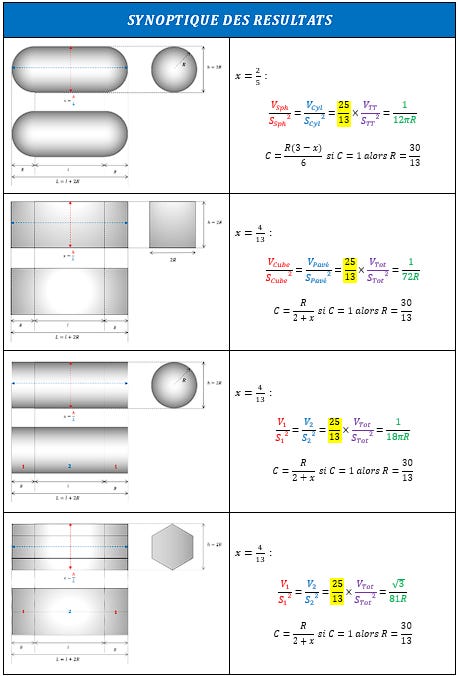
Après d’innombrables tentatives pour essayer d’en découvrir plus, j’ai envisagé la possibilité que la relation ne soit pas propre uniquement au TIC TAC. J’ai donc appliqué la relation à d’autres formes « géométriquement voisines ». Je vous laisse juger les résultats :
Détails des calculs de chaque forme disponibles en annexe 5.
En appliquant la relation à des formes différentes, on obtient des valeurs de x différentes mais on retrouve pourtant le même coefficient 25/13 ! Il semble donc que ce que nous considérions initialement pour une relation propre à une seule forme géométrique soit en réalité un principe applicable à différentes formes.
Par commodité, je me suis permis de le nommer « Principe d’Affinité Géométrique » ou PAG en référence à une 3ème partie inachevée.
A ce jour, j’envisage la possibilité que ce principe permettrait de catégoriser les formes selon leurs symétries. Il serait peut-être ainsi possible de catégoriser la famille des 25/13 ou d’autres familles restant à découvrir. L’origine de ce principe pourrait également provenir d’une conséquence des groupes de LIE voire de l’application d’un Lagrangien à une relation encore indéterminée.
Quoiqu’il en soit le Principe d’Affinité Géométrique est un objet mathématique pur et indépendant du phénomène qui nous a mis sur sa piste. Il s’agit d’un problème mathématiques propre à part entière et qui doit être abordé, exploré en analysé en tant que tel. La forme du TIC TAC ne serait à priori qu’une application du Principe d’Affinité Géométrique. S’intéresser au seul cas du TIC TAC peut donc s’assimiler à n’observer qu’une seule face d’un dé dont nous ignorons encore l’envergure réelle.
Il n’en demeure pas moins stupéfiant et même choquant que la simple curiosité mathématique appliquée à un cas de PAN ait pu déboucher sur une telle découverte…
Nous nous interrogions sur la nature de l’avantage ayant pu prévaloir sur l’aérodynamisme. Etant donné que ces travaux n’ont jusqu’à présent fait ressurgir aucune constante de la physique, que la littérature ne fait aucune mention de la relation, nous ne sommes pas en mesure de relier notre relation à une quelconque nécessité physique ou technique. Malgré des progrès significatifs, cet aspect demeure une énigme.
ANNEXE 1 : Calculs
ANNEXE 2 : Expressions des volumes et des surfaces de chaque partie et de l’ensemble
ANNEXE 3 : Vérifications sur la relation V/S²
Pour la valeur de x= 0,4 et seulement pour cette valeur, le tableau de comparaison fait émerger une relation remarquable propre à la géométrie du Tic-Tac :
En reprenant notre premier tableau (avant que la valeur de x=0.4 ne soit prise en compte) on peut établir l’équation initiale :
On notera que cette relation est indépendante de et ne dépend que de x.
Quelles sont les solutions de cette relation ? En développant on obtient :
donc
ce qui donne l’équation du second degré :
Donc de la forme :
dont le discriminant s’écrit :
on en déduit les racines :
On retrouve donc x=0,4 en parfaite concordance avec les observations de la vidéo FLIR1
Solution sphérique (Correspond à une solution où l=0)
La résolution de la relation V/S² mène à une solution particulière de x correspondant précisément à la valeur observée sur la vidéo. Il est donc très improbable que cette solution particulière apparaisse de façon fortuite.
ANNEXE 4 : Extension de la relation
Calculons les rapports indiqués dans la première colonne avant de les exprimer en fonction de la surface ou du volume du TIC TAC en deuxième colonne :
A l’aide de ces nouvelles expressions et des rappels, exprimons les termes de la relation V/S² en fonction de STT et VTT :
Par application de la relation V/S² , nous obtenons :
Vérifions pour quelle(s) valeur(s) de x l’égalité entre les 3èmes et 5èmes termes sont valables en résolvant :
On retrouve de façon concordante la valeur x= 0,4 ; ce qui vient conforter nos hypothèses et déductions précédentes. Calculons à présent la valeur des termes :
Il est ainsi démontré que pour la valeur particulière x=0,4 ; on peut appliquer la relation :
Notons bien que cette formulation ne présume en aucune façon de la valeur de R.
ANNEXE 5 : Calculs applications du principe d’Affinité Géométrique à différentes formes
TIC TAC
Rappelons la schématisation du phénomène :
Rappelons l’expression de l :
En première partie, nous avions mis en évidence la valeur particulière x :
L’égalité de l’affinité géométrique entre les parties est donc soumise à la condition x= 2/5 .
Comparons à présent l’affinité géométrique de l’ensemble à celles de chaque partie :
Nous en concluons que pour la forme du Tic-Tac la relation d’affinité géométrique s’écrit :
PRISME A SECTION CARREE
Schématisation la forme :
Comme pour le cas du Tic-Tac, seule la surface donnant sur l’extérieur est prise en compte.
Pour quelle valeur de x peut-on observer l’égalité des affinités géométriques entre parties :
Comparons l’affinité géométrique de l’ensemble à celles de chaque partie :
De façon absolument stupéfiante, on retrouve donc la relation d’affinité géométrique avec le même facteur 25/13 :
Le facteur 25/13 correspondrait-il à une constante vers laquelle convergent les affinités géométriques sous certaines conditions ?
A toutes fins utiles sont ajoutées quelques observations intéressantes :
Calculons la compacité :
Pour x = 4/13 :
Il vient que si la compacité est de 1 alors R vaut exactement 30/13 comme pour le cas du Tic-Tac…
Il est très étonnant de retrouver tant de résultats communs entre 2 formes si différentes.
Notons par ailleurs que :
CYLINDRE
La forme n’est pas sans rappeler certains cas de PAN en forme de « cigares ».
Schématisation la forme ainsi :
Comme pour le cas du Tic-Tac, seule la surface donnant sur l’extérieur est prise en compte.
Pour quelle valeur de x peut-on observer l’égalité des affinités géométriques des parties :
Comparons l’affinité géométrique de l’ensemble à celles de chaque partie :
De façon tout aussi stupéfiante, on retrouve une nouvelle fois la relation d’affinité géométrique avec le même facteur 25/13 :
A toutes fins utiles sont ajoutées quelques observations intéressantes :
Calculons la compacité :
Puisqu’ici aussi x= 4/13 :
De même si C=1 alors R= 30/13 encore une fois exactement comme pour le cas du Tic-Tac.
De façon stupéfiante, il vient que la compacité du cylindre est exactement la même que celle du pavé à section carrée précédent.
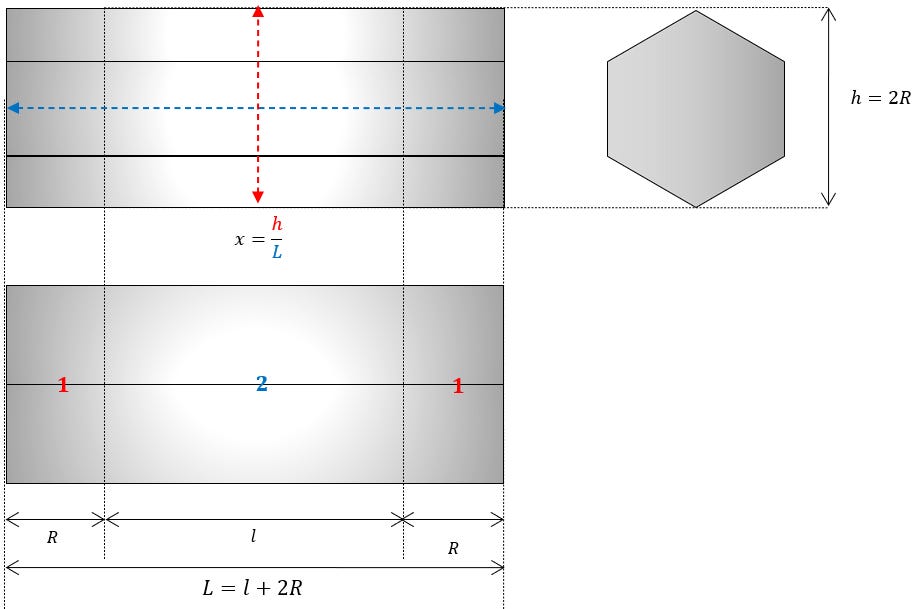
PRISME A SECTION HEXAGONALE
Schématisation la forme ainsi :
Comme pour les cas précédents, seule la surface donnant sur l’extérieur est prise en compte.
Dans ces conditions, le rayon interne de l’hexagone vaut :
Pour quelle valeur de x peut-on observer l’égalité des affinités géométriques des parties :
Comparons l’affinité géométrique de l’ensemble à celles de chaque partie :
Toujours avec le même étonnement, on retrouve une nouvelle fois la relation d’affinité géométrique avec le même facteur 25/13 :
Seul le dernier terme semble suggérer une variation en fonction de la forme géométrique. Il est très surprenant de constater le succès de la relation d’affinité géométrique sur ces quelques essais.
A toutes fins utiles sont ajoutées quelques observations intéressantes :
Calculons la compacité :
Puisqu’ici aussi x = 4/13 :
De même si C=1 alors R= 30/13 encore une fois exactement comme pour le cas du Tic-Tac.
De façon stupéfiante, il vient que la compacité du prisme hexagonal est exactement la même que celle du pavé à section carrée et du triple cylindre.